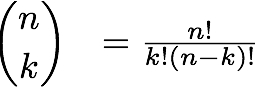Archive
Car Talk Puzzler #5: The Perfect Square Dance
PUZZLER: The Perfect Square Dance!
Sally invited 17 guests to a dance party. She assigned each guest a number from 2 to 18, keeping 1 for herself. The sum of each couple’s numbers was a perfect square. What was the number of Sally’s partner?
The fifth in my ongoing series of solving Car Talk Puzzlers with my programming language of choice. I’m using Python again, just like last time.
There are a few pieces to this. The first is, how do we generate a list of all possible pairs that match the perfect square constraint? With list comprehensions and a helper function this is easy.
def perfect_square(n): return math.sqrt(n) == int(math.sqrt(n)) # range creates a list that's exclusive of last number. Thus to go from 1 to n, # use range(1, n+1) guests = range(1, num_guests + 1) # By enforcing the x# a whole bunch of equivalent pairs (e.g. (3,6) and (6,3)). pairs = [(x,y) for x in guests for y in guests if x<y and perfect_square(x+y)] >>> guests [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18] >>> pairs [(1, 3), (1, 8), (1, 15), (2, 7), (2, 14), (3, 6), (3, 13), (4, 5), (4, 12), (5, 11), (6, 10), (7, 9), (7, 18), (8, 17), (9, 16), (10, 15), (11, 14), (12, 13)]
>>> itertools.combinations([1,2,3,4,5], 2) # This is a sort of generator object which lazily returns the values as needed. # To force them to all be evaluated at once, to see how this works, # wrap the call in a list function. >>>list(itertools.combinations([1,2,3,4,5],2)) [(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)]
This performs exactly as how we would expect. Note that I want combinations rather than permutations because the order does not matter.
Yeah, I think we can handle checking 48620 combinations.
def flatten(nested): """ Flatten one level of nesting. Returns a generator object For instance: list(flatten([(1,3),(5,6)])) --> [1,3,5,6] """ return itertools.chain.from_iterable(nested) def all_guests_present_once(combination): """ Returns whether each guest is present once Combination is a list of tuples, e.g. [(1,5),(7,8)] """ flattened = list(flatten(combination)) return len(set(flattened)) == len(flattened) >>> all_guests_present_once([(1,3),(4,5)]) True >>> all_guests_present_once([(1,3),(3,6)]) False
OK we’re ready to throw it all together.
def dance_arrangement(num_guests):
"""
Returns a valid pairing for all guests if possible, else an empty set
"""
# Clearly you need an even number of guests to have everyone paired
if num_guests % 2 == 1:
return []
else:
# range creates a list that's exclusive of last number. Thus to go from 1 to n,
# use range(1, n+1)
guests = range(1, num_guests + 1)
# By enforcing the x # a whole bunch of equivalent pairs (e.g. (3,6) and (6,3)).
pairs = [(x,y) for x in guests for y in guests if x # brute force search
all_arrangements = itertools.combinations(pairs, num_guests / 2)
return filter(all_guests_present_once, all_arrangements)
Running the program with num_guests = 18, we get
[((1, 15), (2, 14), (3, 13), (4, 12), (5, 11), (6, 10), (7, 18), (8, 17), (9, 16))]
8 [((1, 8), (2, 7), (3, 6), (4, 5))] 14 [((1, 8), (2, 14), (3, 13), (4, 12), (5, 11), (6, 10), (7, 9))] 16 [((1, 8), (2, 7), (3, 6), (4, 5), (9, 16), (10, 15), (11, 14), (12, 13))] 18 [((1, 15), (2, 14), (3, 13), (4, 12), (5, 11), (6, 10), (7, 18), (8, 17), (9, 16))]
As you can see, 8, 14, and 16 guests can also be paired up in this way. Something to keep in mind the next time you are going to have a party.
Full sourcecode can be found on Github.
Car Talk Puzzler #4: Flipping Ages
RAY: This was sent in many weeks ago by Wendy Gladstone, and as usual I tweaked it a little bit.
She writes: “Recently I had a visit with my mom and we realized that the two digits that make up my age when reversed resulted in her age. For example, if she’s 73, I’m 37. We wondered how often this has happened over the years but we got sidetracked with other topics and we never came up with an answer.
“When I got home I figured out that the digits of our ages have been reversible six times so far. I also figured out that if we’re lucky it would happen again in a few years, and if we’re really lucky it would happen one more time after that. In other words, it would have happened 8 times over all. So the question is, how old am I now?”
Here’s the fourth in my Car Talk Puzzler series; today I’m going to be using Python because it’s my current favorite language, and because it’s well suited to filtering, mapping, etc. I won’t put too much commentary here.
# Find all the ages such that the second age is the reverse of the first age. Don't worry that there are a lot of impossibilities; we'll fix it through filtering # Note that [::-1] is the slice operator that says iterate backwards through the string; this effectively reverses the list. matching_ages = map(lambda x:(x, int(str(x)[::-1])), range(0,100)) matching_ages # OUT: [(0, 0), (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (7, 7), (8, 8), (9, 9), (10, 1), (11, 11), (12, 21), (13, 31), (14, 41), (15, 51), (16, 61), (17, 71), (18, 81), (19, 91), (20, 2), (21, 12), (22, 22), (23, 32), (24, 42), (25, 52), (26, 62), (27, 72), (28, 82), (29, 92), (30, 3), (31, 13), (32, 23), (33, 33), (34, 43), (35, 53), (36, 63), (37, 73), (38, 83), (39, 93), (40, 4), (41, 14), (42, 24), (43, 34), (44, 44), (45, 54), (46, 64), (47, 74), (48, 84), (49, 94), (50, 5), (51, 15), (52, 25), (53, 35), (54, 45), (55, 55), (56, 65), (57, 75), (58, 85), (59, 95), (60, 6), (61, 16), (62, 26), (63, 36), (64, 46), (65, 56), (66, 66), (67, 76), (68, 86), (69, 96), (70, 7), (71, 17), (72, 27), (73, 37), (74, 47), (75, 57), (76, 67), (77, 77), (78, 87), (79, 97), (80, 8), (81, 18), (82, 28), (83, 38), (84, 48), (85, 58), (86, 68), (87, 78), (88, 88), (89, 98), (90, 9), (91, 19), (92, 29), (93, 39), (94, 49), (95, 59), (96, 69), (97, 79), (98, 89), (99, 99)] # Here we filter by only allowing matches in which the mother's age is greater than that of the child. Note the use of a lambda expression, basically an anonymous function. filtered1 = filter(lambda (mother,child):mother > child, matching_ages) filtered1 # OUT: [(10, 1), (20, 2), (21, 12), (30, 3), (31, 13), (32, 23), (40, 4), (41, 14), (42, 24), (43, 34), (50, 5), (51, 15), (52, 25), (53, 35), (54, 45), (60, 6), (61, 16), (62, 26), (63, 36), (64, 46), (65, 56), (70, 7), (71, 17), (72, 27), (73, 37), (74, 47), (75, 57), (76, 67), (80, 8), (81, 18), (82, 28), (83, 38), (84, 48), (85, 58), (86, 68), (87, 78), (90, 9), (91, 19), (92, 29), (93, 39), (94, 49), (95, 59), (96, 69), (97, 79), (98, 89)] # Assume that the mother was at least 15 when she had the kid, and no more than 60 filtered2 = filter(lambda(mother, child):mother-child >= 15 and mother-child < 60, filtered1) filtered2 # OUT: [(20, 2), (30, 3), (31, 13), (40, 4), (41, 14), (42, 24), (50, 5), (51, 15), (52, 25), (53, 35), (60, 6), (61, 16), (62, 26), (63, 36), (64, 46), (71, 17), (72, 27), (73, 37), (74, 47), (75, 57), (82, 28), (83, 38), (84, 48), (85, 58), (86, 68), (93, 39), (94, 49), (95, 59), (96, 69), (97, 79)] len(filtered2) # OUT: 30 # Create a new list comprised of the differences in age between mother and child age_diff = map(lambda(mother,child):mother-child, filtered2) age_diff # OUT: [18, 27, 18, 36, 27, 18, 45, 36, 27, 18, 54, 45, 36, 27, 18, 54, 45, 36, 27, 18, 54, 45, 36, 27, 18] sorted(age_diff) # OUT: [18, 18, 18, 18, 18, 18, 18, 27, 27, 27, 27, 27, 27, 36, 36, 36, 36, 36, 45, 45, 45, 45, 54, 54, 54] # The puzzler states that it's will happen a total of 8 times; that matches the age difference of 18 years filter(lambda(mother,child):mother-child == 18, filtered3) # OUT: [(20, 2), (31, 13), (42, 24), (53, 35), (64, 46), (75, 57), (86, 68), (97, 79)]
Thus the mother is currently 75 years old and the daughter is 57. Tada
Car Talk Puzzler #2: What do these words have in common? An imperative and functional approach using Java and Scala
Here’s the second in my series of Car Talk puzzler solutions. Today I’m going to be illustrating a solution first in Java, and then in Scala in order to show how functional programming features can drastically reduce the number of lines of code, while still expressing the developer’s intent.
RAY: Here’s the answer. If you notice, the first letter in each of the words is from farther down in the alphabet than all the subsequent letters. And if we assigned a number to every letter in the alphabet, so that A is one, B is two, C is three and so on…
TOM: Yeah, yeah, yeah.
RAY: Then the numerical place in the alphabet of the first letter is equal to the sum of the numerical places of all the other letters. For example, Table: T is 20, A is 1, B is 2, L is 12, E is 5, so 1 plus 2 plus 12 plus 5 –
TOM: Is 20.
So, we have the answer. But as the guys mention on the show, there are probably other words as well. Let’s do a brute force search through the dictionary to find all such words. The dictionary I”ll be using is available here, as a new line separated list of words, one per line. This makes it very easy to deal with.
Here’s the rather straightforward solution in Java:
import java.io.FileReader;
import java.io.BufferedReader;
import java.io.FileNotFoundException;
import java.io.IOException;
/**
* Determines all the words such that the first letter's ordinal position
* equals the sum of the remaining letters' ordinal positions. For instance,
* "table"'s ordinal numbers are [20,1,2,12,5], and 20 = 1+2+12+5. Thus
* "table" has this property.
*/
public class OrdinalPositionPuzzlerSolver {
/**
* Assumes the string consists just of A-Z, a-z.
*/
public static boolean hasProperty(String s) {
if (s.length() < 2) {
return false;
}
char[] letters = s.toCharArray();
int sum = 0;
for (int i = 1; i < letters.length; i++) {
int ordinal = ordinal(letters[i]) ;
sum += ordinal;
}
return sum == ordinal(letters[0]);
}
/**
* @return the 1 based ordinal position of the letter. For instance,
* a is 1, b is 2, etc.
*/
public static int ordinal(char letter) {
return Character.toLowerCase(letter) - 'a' + 1;
}
public static void main(String[] args) {
String dictionaryPath = "dict.txt";
/**
http://www.javapractices.com/topic/TopicAction.do?Id=42
*/
try {
BufferedReader input = new BufferedReader(new FileReader(dictionaryPath));
try {
String line = null;
while (( line = input.readLine()) != null){
if (hasProperty(line)) {
System.out.println(line);
}
}
}
catch (FileNotFoundException e) {
System.err.println("Error, file " + dictionaryPath + " didn't exist.");
}
finally {
input.close();
}
}
catch (IOException e) {
System.err.println("IO Error:" + e);
}
}
}
The only place that bears some explanation might be the ordinal function:
/**
* @return the 1 based ordinal position of the letter. For instance,
* a is 1, b is 2, etc.
*/
public static int ordinal(char letter) {
return Character.toLowerCase(letter) - 'a' + 1;
}
Basically, letters (characters) in Java are really just numbers under the hood which get mapped back into letters when printed to the screen. So, we can do arithmetic using letters. ‘a’ + 1 = ‘b’, ‘b’ + 2 = ‘d’, and so on. (This only works because the letters a-z and A-Z are mapped to a continuous range of integers). So if we want to convert a->1, first we figure out a’s position from the start of the alphabet (‘a’ -‘a’ == 0, it’s the first), and add 1 to get the 1-based number.
The other thing to notice is how much junk code there is just to read the lines from our file:
try {
BufferedReader input = new BufferedReader(new FileReader(dictionaryPath));
try {
String line = null;
while (( line = input.readLine()) != null){
if (hasProperty(line)) {
System.out.println(line);
}
}
}
catch (FileNotFoundException e) {
System.err.println("Error, file " + dictionaryPath + " didn't exist.");
}
finally {
input.close();
}
}
catch (IOException e) {
System.err.println("IO Error:" + e);
}
Believe it or not, this is relatively idiomatic Java code to accomplish this task. First we wrap a file reader in a buffered reader so that we do not continuously access the file; rather we read chunks into the file and buffer them for in-memory access. That’s 20 lines of code just to iterate over the lines of a file, determine if they match a pattern, and print it to the terminal.
It really should not be this hard.
As I’ve said before, Java’s verbosity is one of my biggest complaints about it. The program works, and it’s relatively straightforward, but it can’t really be described as elegant. In that same post I mentioned my interest in Scala as an alternative to Java. It’s a compiled language that runs in the JVM, but through its type inferencing and functional language aspects, it is much more concise; the creator Martin Odersky claims a typical Source Line of Code (SLOC) reduction of 2x between equivalent Scala and Java programs. Let’s reimplement the program in Scala, and see if this claim rings true. (Note: I’m not an expert in scala so there’s probably even more concise, idiomatic ways to accomplish what I’m trying to do. But let’s start somewhere).
The syntax of scala is very similar to that of Java. One of the main differences is that type declarations occur after the variable rather than before.
int x = 0; // Java val x: Int = 0 // Scala
Another syntactic difference is that generic type arguments occur within square brackets rather than angle brackets
List<Integer> intList = ...; // java val intList: List[Int] = ..// scala
Because of this, array indexing is done through use of parentheses rather than square brackets.
// Java
int[] x = {1,2,3,4};
x[0] // 1
// Scala val x: List[Int] = List(1,2,3,4) x(0) // 1
Due to type inferencing, you often don’t need to declare the type of your variables; the compiler can figure it out. Thus the last declaration could be rewritten as
val x = List(1,2,3,4)
I highly recommend you watch Martin Odersky’s introduction to Scala video; it’s about an hour long and goes over the design considerations and differences from Java.
There are no static functions in Scala; rather you create a singleton object through the keyword ‘object’ and access the method in the same way.
Finally, there is a read/eval/execute interpreter built-in, accessible by calling ‘scala‘ in the command line. This allows you to experiment without having to explicitly compile any code; it allowed me to create the pieces iteratively before plunking them into a file for later compilation.
scala
Welcome to Scala version 2.7.3.final (Java HotSpot(TM) Client VM, Java 1.5.0_22).
Type in expressions to have them evaluated.
Type :help for more information.
scala> 1+1
res0: Int = 2
scala> print("hello world")
hello world
scala>
OK, enough beating around the bush. Let’s solve this puzzler!
We’ll tackle this in 3 parts.
1) Summing a list of numbers
2) Completing the ordinal number function
3) Iterating over all the lines in the dictionary file
Summing a list of numbers
A first pass at a sum function might be as follows:
def sum(nums: Iterable[Int]): Int = {
var sum = 0
for (num <- nums) {
sum += num
}
sum
}
Note the declaration of sum as a var as opposed to a val; a val is equivalent to a final value while a var can be reassigned. Why did I declare the nums argument to be of type Iterable rather than List? Well, a List is iterable. So is an array. So are any number of things. We want to keep this function as generic as possible. Pasting this into our interpreter, we can test this out.
scala> def sum(nums: Iterable[Int]): Int = {
| var sum = 0
| for (num <- nums) {
| sum += num
| }
| sum
| }
sum: (Iterable[Int])Int
scala> sum(List())
res4: Int = 0
scala> sum(List(1,2,3,4,5))
res5: Int = 15
scala> sum(Array(1,2,3,4))
res6: Int = 10
This works, but let’s look at another way to solve this problem – a functional rather than imperative solution. Java is inherently imperative, meaning you’ll see a lot of explicit while and for loops. Here’s just a quick excerpt of each the wikipedia articles to define each programming paradigm:
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state.
In computer science, imperative programming is a programming paradigm that describes computation in terms of statements that change a program state. In much the same way that imperative mood in natural languages expresses commands to take action, imperative programs define sequences of commands for the computer to perform.
So whereas the imperative manner is completely explicit in how the sum is created, using a mutable state variable (sum), a more functional approach will eliminate the use of mutable state altogether.
The reduce function is absolutely crucial to understand in order to program in a functional manner; let’s examine Python’s definition of it before applying it to the problem at hand.
Here is the Python definition of reduce function:
reduce(function, iterable[, initializer])
Apply function of two arguments cumulatively to the items of iterable, from left to right, so as to reduce the iterable to a single value. For example, reduce(lambda x, y:x+y, [1, 2, 3, 4, 5]) calculates ((((1+2)+3)+4)+5). The left argument, x, is the accumulated value and the right argument, y, is the update value from the iterable. If the optional initializer is present, it is placed before the items of the iterable in the calculation, and serves as a default when the iterable is empty. If initializer is not given and iterable contains only one item, the first item is returned.
And the description of the built-in sum function is as follows:
sum(iterable[, start])¶
Sums start and the items of an iterable from left to right and returns the total. start defaults to 0. The iterable‘s items are normally numbers, and are not allowed to be strings. The fast, correct way to concatenate a sequence of strings is by calling ”.join(sequence). Note that sum(range(n), m) is equivalent to reduce(operator.add,range(n), m) To add floating point values with extended precision, see math.fsum().
While Scala doesn’t have a built-in sum function, it does have support for reducing a list through use of a function. It has both a reduce left (left to right reduction) and reduce right (right to left reduction). Here is Scala’s definition of reduceLeft:
def reduceLeft[B >: A](op : (B, A) => B) : B
Combines the elements of this iterable object together using the binary operator op, from left to right
Notes Will not terminate for infinite-sized collections.
Parameters op – The operator to apply
Returns op(… op(a0,a1), …, an) if the iterable object has elements a0, a1, …, an.
Throws Predef.UnsupportedOperationException – if the iterable object is empty.
This might be a little confusing but bear with me.
First, we need to write a binary function for our sum operator – after all, we want to pairwise reduce the list by using an add operator. A first pass is as follows:
scala> def add(x: Int, y: Int): Int = { x + y }
add: (Int,Int)Int
scala> List(1,2,3,4).reduceLeft(add)
res12: Int = 10
scala> List().reduceLeft(add)
java.lang.UnsupportedOperationException: Nil.reduceLeft
at scala.List.reduceLeft(List.scala:1093)
at .(:6)
at .()
at RequestResult$.(:3)
at RequestResult$.()
at RequestResult$result()
at sun.reflect.NativeMethodAccessorImpl.invoke0(Native Method)
at sun.reflect.NativeMethodAccessorImpl.invoke(NativeMethod...
scala> List(-5,5).reduceLeft(add)
res14: Int = 0
Note that you cannot call sum on an empty list any more; doing so results in an UnsupportedOperationException. This is arguably more correct than returning 0, but we will have to ensure that we don’t attempt to sum an empty iterable object.
So a working sum definition would be
def sum(nums: Iterable[Int]): Int = {
def add(x: Int, y: Int): Int = { x + y }
nums.reduceLeft(add)
}
Note that you can nest function definitions, as functions are objects in Scala, and thus can be defined wherever a variable could. Note too that I never have to explicitly return a value; the last evaluated value is implicitly returned by the function.
Finally, if you want to be even more terse, you can replace the explicitly defined add function with an anonymous one:
def sum(nums: Iterable[Int]): Int = {
nums.reduceLeft(_+_)
}
Read the Daniel Spiewak’s excellent blog post for a better explanation for what’s going on here. Here’s a quick explanation:
Completing the ordinal number functional
Recall the function that we had in Java for computing the ordinal position of each letter:
public static boolean hasProperty(String s) {
if (s.length() < 2) {
return false;
}
char[] letters = s.toCharArray();
int sum = 0;
for (int i = 1; i < letters.length; i++) {
int ordinal = ordinal(letters[i]) ;
sum += ordinal;
}
return sum == ordinal(letters[0]);
}
/**
* @return the 1 based ordinal position of the letter. For instance,
* a is 1, b is 2, etc.
*/
public static int ordinal(char letter) {
return Character.toLowerCase(letter) - 'a' + 1;
}
Again, we could directly translate this code into Scala but doing so would not be making full use of Scala’s functional underpinnings. We are converting from characters of the string to their ordinal positions in the alphabet. While the Java code does this one letter at a time, keeping a sum, it’s just as correct to do the entire mapping process and then sum over the new list. Pictorially:
Just as there is a reduce function to convert an iterable object into a single entry, so too is there a function to convert an Iterable of one type into an Interable of another; it is the map function.
// The underscore in an anonymous function like this is a placeholder for the entry in the iterable collection currently being processed
scala> List(1,3,4).map(_+5)
res19: List[Int] = List(6, 8, 9)
scala> List("hi","there").map(_.toUpperCase())
res22: List[java.lang.String] = List(HI, THERE)
The above examples map from Int-> Int and String->String but there’s nothing stopping us from converting types.
scala> List(100,300,400).map(_.toString()) res23: List[java.lang.String] = List(100, 300, 400)
Finally, let’s apply the ordinal function to a string:
scala> "cat".map(Character.toLowerCase(_) - 'a' + 1) res24: Seq[Int] = ArrayBufferRO(3, 1, 20)
Thus the entire function for determining if the word is a match is
[sourecode language=”scala”]
/**
* Determines if the word has the desired property of the ordinal position
* of first letter equalling the sum of the ordinal positions of the other
* letters
* Expects letters in the range [a-zA-Z];
*/
def matches(word: String): Boolean = {
if (word.length() < 2) {
false
}
else {
val ordinals = word.map(Character.toLowerCase(_) – 'a' + 1)
val ordinalSum = sum(ordinals.drop(1))
ordinals(0) == ordinalSum
}
}
[/sourecode]
Iterating over the lines in a file
Remember how it took 20 lines to iterate over all the lines in a file? Fortunately Scala makes it incredibly easy:
val lines = scala.io.Source.fromFile("dict.txt").getLines
The variable is actually not an array or a list; it is an iterator over the lines in the file. But iterators are still iterable, so all of our previously mentioned functions for dealing with iterable objects still work. Again, rather than looping over each element, explicitly testing, and printing whether it matched, we will use a functional approach, namely the ‘filter’ function.
scala> List(1,2,3,4).filter(_%2==0) res25: List[Int] = List(2, 4)
The function passed into filter must return Boolean; since our matches() function does that, we can insert it right in:
val lines = scala.io.Source.fromFile("dict.txt").getLines
val matching = lines.filter(matches)
matching.foreach(print(_))
When we run the complete code, we get the following list of matches:
- acknowledgements
approximation
bumptiously
capitalizations
circuitously
conceptualizing
consciousness
consistently
credulousness
crystallizing
disconcertingly
discriminatory
electrocutions
excommunication
existentialism
experimentally
exploitations
expressively
extraneously
governmentally
impersonations
incomprehensibly
indispensability
initializations
intercommunicated
interpolations
notwithstanding
organizationally
oversimplifying
phenomenologically
sportswriting
Wait a minute… what’s going on here? These obviously don’t follow the pattern. Let’s open a terminal and do some testing.
First we paste our two helper method definitions in
Welcome to Scala version 2.7.3.final (Java HotSpot(TM) Client VM, Java 1.5.0_22).
Type in expressions to have them evaluated.
Type :help for more information.
scala> def sum(nums: Iterable[Int]): Int = {
| nums.reduceLeft[Int](_+_)
| }
sum: (Iterable[Int])Int
scala>
scala> /**
| * Determines if the word has the desired property of the ordinal position
| * of first letter equalling the sum of the ordinal positions of the other
| * letters
| * Expects letters in the range [a-zA-Z];
| */
scala> def matches(word: String): Boolean = {
| val ordinals = word.map(Character.toLowerCase(_) - 'a' + 1)
| val ordinalSum = sum(ordinals.drop(1))
| ordinals(0) == ordinalSum
| }
matches: (String)Boolean
scala> matches("table")
res0: Boolean = true
scala> matches("chair")
res1: Boolean = false
scala> matches("consistently")
res2: Boolean = false
This is very strange. “consistently” is one of the words on the list, but it doesn’t pass the test on its own. In fact, none of them do.
What’s the problem? After googling and debugging for a bit, I realized that the precondition I was assuming in my matches method was being violated; the letters were not in the range [A-Za-z]. How could that be? Well, it turns out that the getLines() method returns the lines in the file – with new lines included!
scala> matches("consistently\r\n")
res5: Boolean = true
(The file had been created on Windows, and thus has a carriage feed as well as a new line marker).
Fortunately there is a method to eliminate whitespace (including control characters like these); it’s known as trim.
We can put the trim in one of two places, either in the matches() method itself,
def matches(word: String): Boolean = {
val ordinals = word.trim().map(Character.toLowerCase(_) - 'a' + 1)
val ordinalSum = sum(ordinals.drop(1))
ordinals(0) == ordinalSum
}
scala> matches("consistently\r\n")
res6: Boolean = false
scala> matches("consistently")
res7: Boolean = false
Or we can introduce the trim while iterating over the lines in the collection. I’ve opted for this second approach; I’m making it a precondition of calling the method matches() that the input is already sanitized. We introduce an implicit mapping from the string to the trimmed version of the string:
// An iterator of lines in the file; note that they have newline control characters
val lines = scala.io.Source.fromFile("dict.txt").getLines
// Filter the lines, eliminating the new lines through trim mapping
val matching = lines.filter(i => matches(i.trim()))
matching.foreach(print(_))
After making the change, the result is
- cab
- hag
- jade
- leaf
- leg
- maced
- mica
- mid
- need
- pig
- real
- ride
- same
- sand
- seam
- sod
- table
- toad
- toe
- vial
- ward
- whack
- who
- wick
- win
- yeas
- yet
- zebra
- zinc
Tada!
The final version of the program is
object OrdinalPositionSolver {
/**
* Determines if the word has the desired property of the ordinal position
* of first letter equalling the sum of the ordinal positions of the other
* letters
* Expects letters in the range [a-zA-Z];
*/
def matches(word: String): Boolean = {
if (word.length() < 2) {
false
}
else {
val ordinals = word.map(Character.toLowerCase(_) - 'a' + 1)
val ordinalSum = sum(ordinals.drop(1))
ordinals(0) == ordinalSum
}
}
def sum(nums: Iterable[Int]): Int = {
nums.reduceLeft[Int](_+_)
}
def main(args: Array[String]) {
// An iterator of lines in the file; note that they have newline control characters
val lines = scala.io.Source.fromFile("dict.txt").getLines
// Filter the lines, eliminating the new lines through trim mapping
val matching = lines.filter(i => matches(i.trim()))
matching.foreach(print(_))
}
}
Conclusion
I have solved the puzzler in two different ways, once in an imperative Java style and once in a more functional Scala style. The functional way is extremely concise and expressive, doing in 30 lines of code what it takes the Java code to do in over 60, confirming the claim that a typical Scala program is at least twice as compact as the corresponding Java program. I have introduced some of the salient syntactic differences between Java and Scala. I have also introduced some of the mainstays of the functional programming paradigm, namely map, reduce, and filter. While there are efforts to make Java more functional, the fact that you cannot pass functions as objects severely inhibits the use of functional programming paradigms.
Car Talk Puzzler #1: The Bank Temperature Sign
One of my favorite podcasts is NPR’s Car Talk, and one of my favorite segments of the show is the weekly puzzler, in which listeners have a week to solve a puzzle that is usually automotive in nature. It struck me that this would be an ideal way to illustrate some beginning programming techniques, while also illustrating some real world problem solving uses of programming. Initially I will be posting solutions in Python, but I will probably show how to do them in other ways as well.
You can see the whole archive of 2010 puzzles, but the specific one I’m starting with can be found here.
In short:
PREVIOUS PUZZLER: Stevie and His Moto
Stevie’s riding his motorcycle to work when he sees a big sign displaying the temperature in Fahrenheit and in centigrade. The digits are exactly reversed. He notices the same thing on the way home. What were the temperatures?
This is an ideal choice for a programming solution because it can be brute forced; a computer can try all possible solutions near instantaneously, something they are very good at. Not all of the puzzlers are so conducive to a programmatic solution.
For those who already know the basics of programming, I’ll post my program first. Afterwards I post explanations more geared towards beginners, but there still is something that more advanced programmers might not know in Python.
Here’s my solution:
def fahrenheitToCelsius(temp): return (temp - 32) / 1.8 def reverseString(s): # Step size is -1, so start at the end and work backwards return s[::-1] # Presumably it was above freezing if it's a spring day LOW_TEMP_FAHRENHEIT = 32 # Presumably it was below 100 degrees HIGH_TEMP_FAHRENHEIT = 100 def main(): for temp in range(LOW_TEMP_FAHRENHEIT, HIGH_TEMP_FAHRENHEIT): # Round the float to nearest whole number, cast to integer celsius = int(round(fahrenheitToCelsius(temp))) # Convert the integers to strings so as to be able to reverse the digits fahrenheitString = str(temp) celsiusString = str(celsius) # See if the reversed digits match if fahrenheitString == reverseString(celsiusString): print temp, celsius if __name__ == '__main__': main()
Spoiler:
python Temperature.py 61 16 82 28
Tada! The program calculated the correct solution.
Let’s break the problem into a few logical steps:
1) Convert a Fahrenheit temperature to Celsius (we’re going to be able to do this in order to determine what the temperature on the signs must have been)
2) Round a number to the nearest whole number (converting Fahrenheit to Celsius will often leave a fractional part, but most signs don’t display temperature in increments smaller than 1 degree)
3) Reverse the digits of a number (in order to tell whether the temperatures are the reverse of each other)
4) Test a whole bunch of Fahrenheit temperatures to discover the matching Celsius ones, using steps 1 – 3.
Let’s explain each part in order.
Convert Fahrenheit to Celsius
The first part is the most straightforward:
def fahrenheitToCelsius(temp): return (temp - 32) / 1.8
There’s not a lot to say about this part; this is the formula to convert from Fahrenheit to Celsius. If you’re new to Python or programming as a whole, this whole block is known as a method declaration; basically methods take in data, do some calculation with the data, and more often than not, return a new piece of data. In our case, we are passing in the temperature in Fahrenheit, and what comes out of it is a temperature in Celsius. Just to show that this indeed works:
Python 2.6.4 (r264:75708, Oct 26 2009, 08:23:19) [MSC v.1500 32 bit (Intel)] on win32 Type "help", "copyright", "credits" or "license" for more information. >>> def fahrenheitToCelsius(temp): ... return (temp - 32) / 1.8 ... >>> fahrenheitToCelsius(212) 100.0 >>> fahrenheitToCelsius(32)
Round a number to nearest whole number
OK, how about rounding a fractional number to the nearest whole number?
Python has a function called, easily enough, round which does exactly that. You choose how many decimal places you want; by default it rounds to 0 (i.e. the nearest whole number)
>>> round (2.252, 2) 2.25 >>> round (2.252 ) 2.0
Notice how even though we round to 0 decimal places, the answer is “2.0”. This is because round returns a double rather than an integer. Integers are what we would think of as “whole numbers” – -1023, 2035, 733, etc. etc. Doubles are an (inexact) representation of a number with a fractional part. It’s a little beyond the scope of this tutorial, but suffice to say there are numbers that a computer cannot represent exactly
>>> round (2.1, 1) 2.1000000000000001
The reason I make the distinction is that we want to treat our numbers as integers; after all we’re rounding them to 0 decimal places, so they are in fact integers. We need the computer to treat them that way. We do this with the int() method
>>> round(2.23501) 2.0 >>> int(2.0) 2
Note too that we can combine these two expressions into one; you’ll often see computer programs written this way, as it allows us to express thoughts more concisely. So the above could be replaced by
>>> int(round(2.23501)) 2
This expression can be read as “after rounding the number to 0 decimal places, convert it to an integer”.
Reverse the digits of a number
How do we reverse the digits of a number? Well, first, we’re going to treat the number as if it were an arbitrary string of letters (characters) rather than numbers. We are going to cast the integer into a string. Strings are a programming concept used to express textual information; they are usually enclosed in quotes.
>>> "hello" 'hello'
The string representation of a number is different than the number itself. For instance, when two strings are “added” together, they become joined (concatenated). When two numbers are added together, they are added in the mathematical sense. For instance
>>> "2" + "2" '22' >>> 2 + 2 4
We are going to treat the numbers as strings because it is fairly easy to reverse the characters of a string, but hard to do so for a number. With a string, you can access each individual character; you cannot (easily) do that with a number. To understand how to reverse the characters of a string, you need to understand a bit about iterating over collections in Python, as well as a concept known as “slice”.
Let’s start with the basic Python data structure known as a list. You can put a heterogenous (mixed) set of objects into a list:
a = [2,3,5,6,"hello","world"]
In this case we’ve put a bunch of numbers, and then two strings into the list data structure. We can get out each element in the list by ‘indexing into’ the array. Unlike in the normal world, in Python you must count starting at 0. So instead of counting 1,2,3,…, you count 0,1,2,… . In other words, if we want to get out the first item we put into the list (the 2), we have to ask for the element at position 0.
>>> a[0] 2
The number within brackets is the index of the element you are accessing from the list.
Now, what if we want the first 3 elements of the list instead of just the first one? To do that, we need to use what’s known as a “slice” in Python. The syntax is [startIndex:endIndex+1]. In other words, if we want the first three elements, those at position 0, 1, and 2, we would ask for
>>> a[0:3] [2, 3, 5]
This can be read as, “start at the element with index 0 and stop before you get to the element with index 3”. Yes, this is a little counter-intuitive – but just stick with me.
What if you want all of the items after a certain point? For instance, I want all the elements including and after the 2nd element. To do that, you omit the second number, but keep the colon. This is saying “start and keep going till you reach the end of the collection”
>>> a[1:] [3, 5, 6, 'hello', 'world']
You can also omit the first number, in which case it is assumed that you want to start at the beginning of the collection
>>> a[:5] [2, 3, 5, 6, 'hello'] >>> a[0:5] [2, 3, 5, 6, 'hello']
What happens if we omit both numbers?
>>> a[:] [2, 3, 5, 6, 'hello', 'world'] >>> a [2, 3, 5, 6, 'hello', 'world']
We get back all the items of the original list! This makes sense if you think about it; we assume we’re starting at the beginning, and we assume we’re ending at the end. Why do I bring this up? Because there’s one last element you can add to take a new slice out of array: the stride argument.
Whereas we’ve been taking some contiguous subset of the list, there’s nothing preventing us from skipping more than one number between every element, in effect taking every second, or every nth number.
>>> a[::2] [2, 5, 'hello']
Interestingly, this number doesn’t have to be positive either; if it’s negative it means we start at the end of the collection and work our way towards the front of the list:
>>> a[::-2] ['world', 6, 3]
Putting this all together then, one way to get the reverse of a list is to take a new slice out of it, taking the whole thing but backwards:
>>> a[::-1] ['world', 'hello', 6, 5, 3, 2]
(More advanced readers: an alternate way, and arguably easier, is to use a list comprehension and the reversed method:
>>> [i for i in reversed(a)] ['world', 'hello', 6, 5, 3, 2]
)
Hopefully you understand how to take slices out of a list now; you can read a whole lot more about slices at any number of sites, including this great introduction to Python.
But why did I start talking about lists? Weren’t we trying to reverse a string, not a list? Well, it turns out you can view a string as a list of individual letters (characters), and treat it exactly the same as we did for lists, including indexing and slicing.
>>> "hello"[0] 'h' >>> "hello"[:3] 'hel' >>> "hello"[::-1] 'olleh'
So, the method for reversing a string (or really any subscriptable object, but that’s another issue) is
def reverseString(s): # Step size is -1, so start at the end and work backwards return s[::-1]
The only thing left to say in this regard is that if we want to convert a number to a string, this is accomplished by the str() method.
Iterate over a range of numbers
We want to test a whole range of temperatures, looking for those that yield the properties desired in the puzzle. Fortunately there is an easy way to generate a list of numbers in a given range in Python: the range command.
</div> >>> range(5) [0, 1, 2, 3, 4] >>> range(5,10) [5, 6, 7, 8, 9] <div>
>>> for x in range(5): ... print x ... 0 1 2 3 4
for temp in range(LOW_TEMP_FAHRENHEIT, HIGH_TEMP_FAHRENHEIT):
Where LOW_TEMP_FAHRENHEIT and HIGH_TEMP_FARENHEIT are two constants defined to limit the range of numbers we are looking at.
Conclusion
I’ve illustrated a brute-force solution to a recent puzzler. Despite being a fairly simple challenge, it illustrates some important features of Python, including range generation, list comprehension, slicing to reverse selections, and converting between different data types.
I’d love to see some other solutions to this problem, so post in the comments if you have ideas.