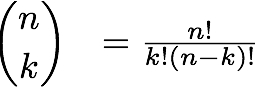Car Talk Puzzler #5: The Perfect Square Dance

PUZZLER: The Perfect Square Dance!

Sally invited 17 guests to a dance party. She assigned each guest a number from 2 to 18, keeping 1 for herself. The sum of each couple’s numbers was a perfect square. What was the number of Sally’s partner?

Puzzler

The fifth in my ongoing series of solving Car Talk Puzzlers with my programming language of choice.  I’m using Python again, just like last time.

There are a few pieces to this.  The first is, how do we generate a list of all possible pairs that match the perfect square constraint?  With list comprehensions and a helper function this is easy.

def perfect_square(n):
  return math.sqrt(n) == int(math.sqrt(n))

# range creates a list that's exclusive of last number.  Thus to go from 1 to n,
# use range(1, n+1)
guests = range(1, num_guests + 1)
# By enforcing the x# a whole bunch of equivalent pairs (e.g. (3,6) and (6,3)).
pairs = [(x,y) for x in guests for y in guests if x<y and perfect_square(x+y)]
>>> guests
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]
>>> pairs
[(1, 3), (1, 8), (1, 15), (2, 7), (2, 14), (3, 6), (3, 13), (4, 5), (4, 12), (5, 11), (6, 10), (7, 9), (7, 18), (8, 17), (9, 16), (10, 15), (11, 14), (12, 13)]

OK great.  At this point I have 18 pairs; 9 of these pairs together form the correct setup.  Now, I could try to be very clever and use logic to deduce the correct pairs.  But I’m lazy and it’s a small problem, so I’m going to use brute force.  I’m just going to take all combinations of 9 pairs and test to see which one uses each guest exactly once.  Not only am I so lazy as to do it this way, I’m not even going to write code to calculate the combinations.  Instead, I’ll use the excellent itertools package.

>>> itertools.combinations([1,2,3,4,5], 2)

# This is a sort of generator object which lazily returns the values as needed.
# To force them to all be evaluated at once, to see how this works,
# wrap the call in a list function.
>>>list(itertools.combinations([1,2,3,4,5],2))
[(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)]

This performs exactly as how we would expect.  Note that I want combinations rather than permutations because the order does not matter.

As I mentioned earlier, I assume that a brute force solution is going to be fast enough.  Let me check my math here.  How many 9-element combinations taken from an 18-element set are there?

N choose K formula - number of k element combinations from set of n elements

Yeah, I think we can handle checking 48620 combinations.

OK, but how do we know whether a given combination (9 pairs of numbers) match our criteria?  The easiest way is to check if the number of unique elements is the same as the number of guests; this indicates that each guest is used only once.  First we flatten our nested list of tuples into a single list, and then use a set to check uniqueness:

def flatten(nested):
  """ Flatten one level of nesting.  Returns a generator object
  For instance:
  list(flatten([(1,3),(5,6)])) --> [1,3,5,6] """
  return itertools.chain.from_iterable(nested)

def all_guests_present_once(combination):
  """ Returns whether each guest is present once
  Combination is a list of tuples, e.g. [(1,5),(7,8)]
  """
  flattened = list(flatten(combination))
  return len(set(flattened)) == len(flattened)

>>> all_guests_present_once([(1,3),(4,5)])
True
>>> all_guests_present_once([(1,3),(3,6)])
False

As you can see, I’m shortcutting a little bit and not checking for the perfect square aspect, since we already did that when constructing our set of pairs.

OK we’re ready to throw it all together.

def dance_arrangement(num_guests):
  """
  Returns a valid pairing for all guests if possible, else an empty set
  """
  # Clearly you need an even number of guests to have everyone paired
  if num_guests % 2 == 1:
    return []
  else:
    # range creates a list that's exclusive of last number.  Thus to go from 1 to n,
    # use range(1, n+1)
    guests = range(1, num_guests + 1)
    # By enforcing the x    # a whole bunch of equivalent pairs (e.g. (3,6) and (6,3)).
    pairs = [(x,y) for x in guests for y in guests if x    # brute force search
    all_arrangements = itertools.combinations(pairs, num_guests / 2)
    return filter(all_guests_present_once, all_arrangements)

Running the program with num_guests = 18, we get

[((1, 15), (2, 14), (3, 13), (4, 12), (5, 11), (6, 10), (7, 18), (8, 17), (9, 16))]

Tada!  Thus Sally’s partner was number 15.

I stumbled onto this page which also sought to solve this problem using programming; it ends with the question

“I wonder if 18 is unique as the total number of dancers which has a solution.  It should be easy to modify the program to check”

It is very easy to modify, and I checked.  I ran the program on all number of guests less than 20, and these are the results:

8 [((1, 8), (2, 7), (3, 6), (4, 5))]
14 [((1, 8), (2, 14), (3, 13), (4, 12), (5, 11), (6, 10), (7, 9))]
16 [((1, 8), (2, 7), (3, 6), (4, 5), (9, 16), (10, 15), (11, 14), (12, 13))]
18 [((1, 15), (2, 14), (3, 13), (4, 12), (5, 11), (6, 10), (7, 18), (8, 17), (9, 16))]

As you can see, 8, 14, and 16 guests can also be paired up in this way.  Something to keep in mind the next time you are going to have a party.

Full sourcecode can be found on Github.